1
1
次の各問に答えよ。
〔問1〕 を計算せよ。
〔問2〕 を計算せよ。
〔問3〕 を計算せよ。
〔問4〕 一次方程式 を解け。
〔問5〕 連立方程式 を解け。
〔問6〕 二次方程式 を解け。
〔問7〕 次の ① と ② に当てはまる数を,下のア〜クのうちからそれぞれ選び,記号で答えよ。
関数 について,の変域が のときのの変域は,
① ②
である。
ア イ ウ エ
オ カ キ ク
〔問8〕 次のの中の「あ」「い」「う」に当てはまる数字をそれぞれ答えよ。
からまでの目の出る大小1つずつのさいころを同時に1回投げる。
大きいさいころの出た目の数を,小さいさいころの出た目の数をとするとき, となる確率は, である。
ただし,大小2つのさいころはともに,からまでのどの目が出ることも同様に確からしいものとする。
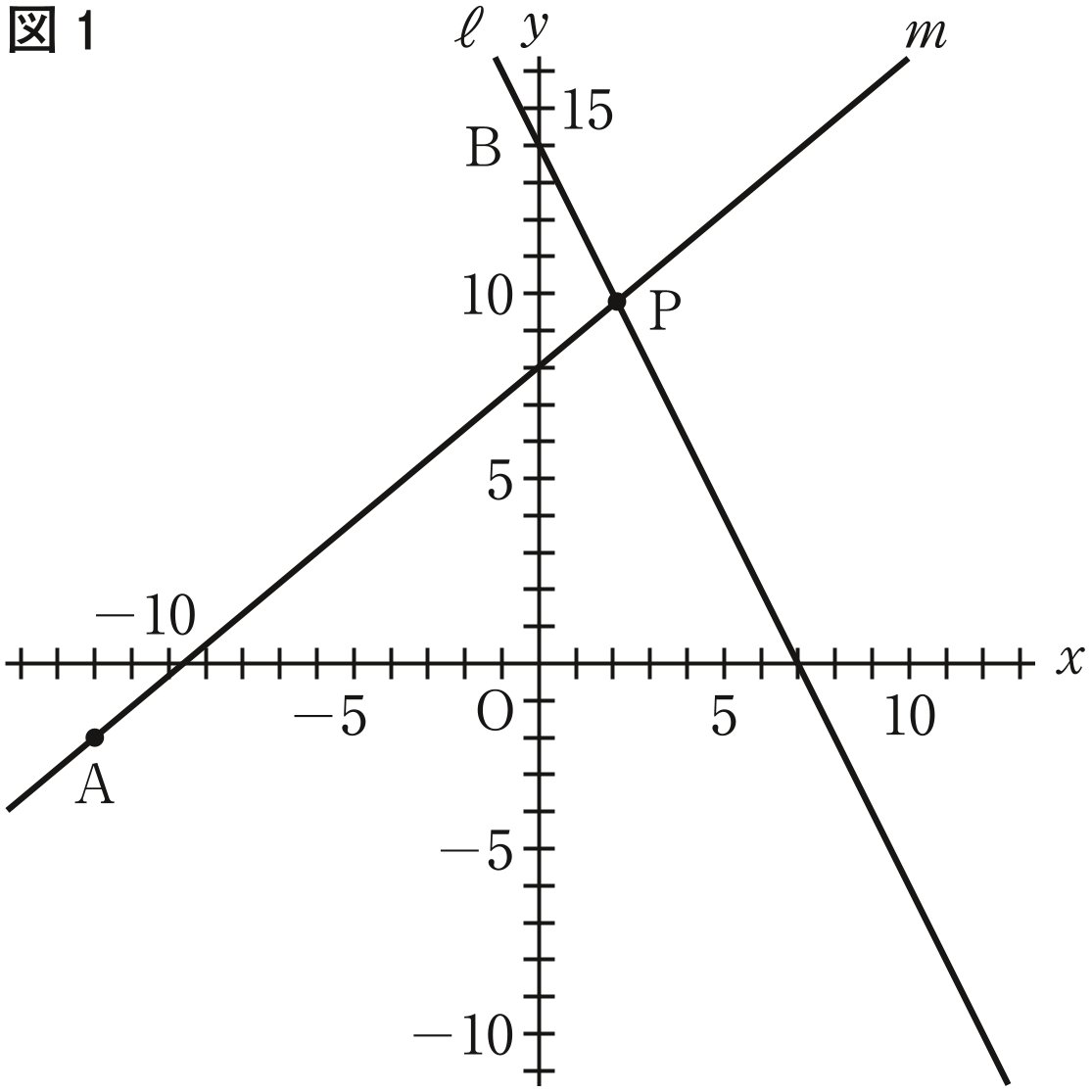
〔問9〕 下の図のように,直線と直線,直線と直線がそれぞれ異なる点で交わっている。
解答欄に示した図をもとにして,直線よりも上側にあり,直線,直線,直線のそれぞれから等しい距離にある点を,定規とコンパスを用いて作図によって求め,点の位置を示す文字も書け。
ただし,作図に用いた線は消さないでおくこと。

![]() で
で
![]() で
で
![]() で
で![]() で
で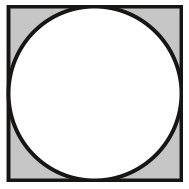
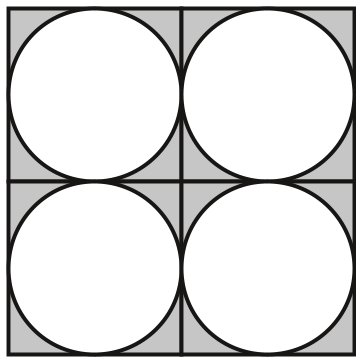
![]() で
で
![]() で
で