7
5
平行四辺形がある。
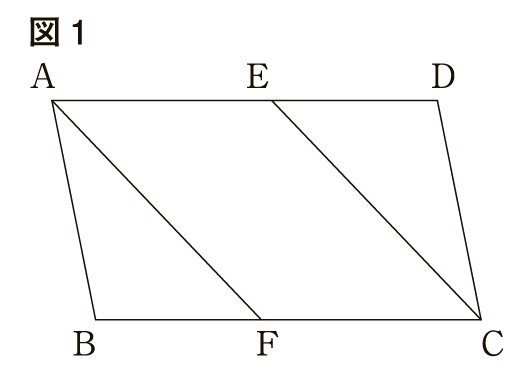
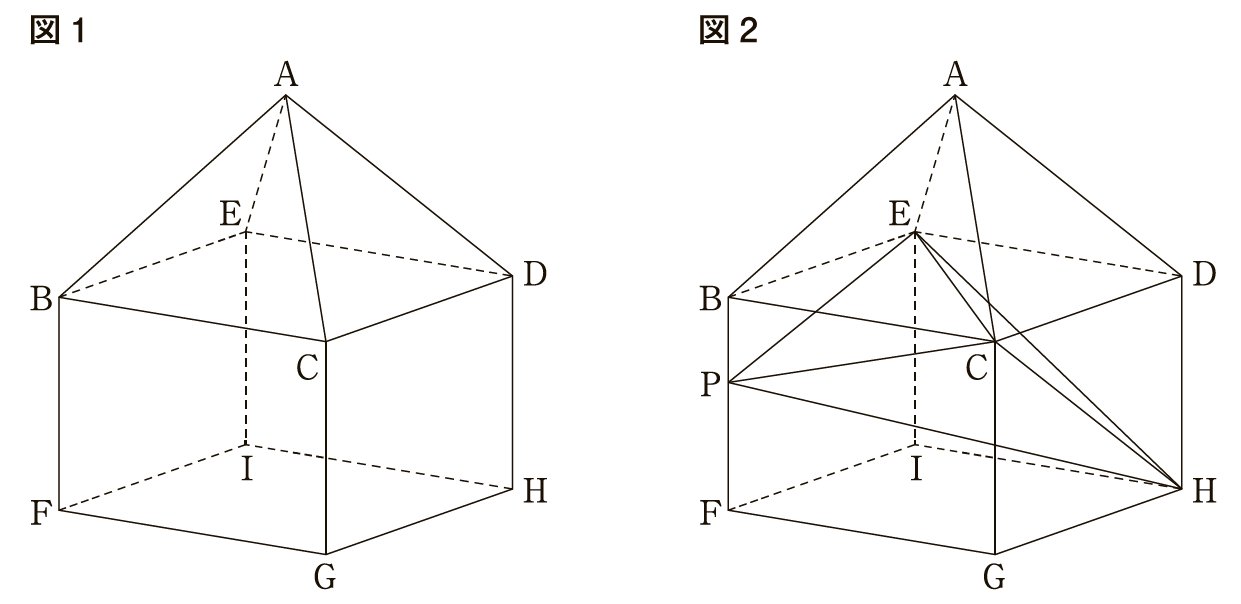
図1のように,線分,上に,点,を, となるようにそれぞれとり,点と点,点と点をそれぞれ結ぶ。
このとき,四角形は平行四辺形である。
次の(1)~(3)に答えよ。
(1) 次は,図1における「四角形は平行四辺形である」ことの証明である。
証明
四角形は平行四辺形だから
ア ・・・①
イ ・・・②
仮定から,
ウ ・・・③
②,③より,
エ
よって,
オ ・・・④
①,④より,
カ1組の向かいあう辺が平行でその長さが等しいので四角形は平行四辺形である。
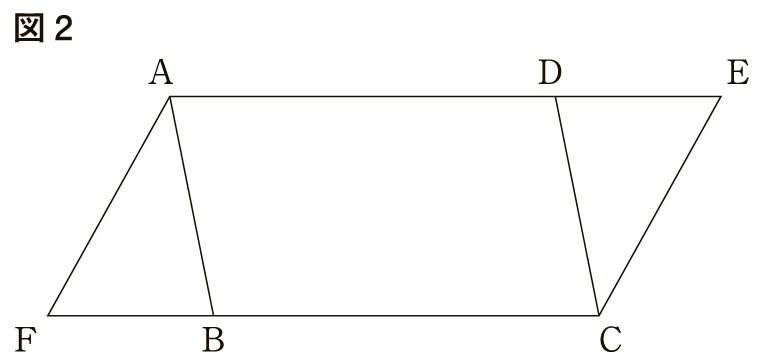
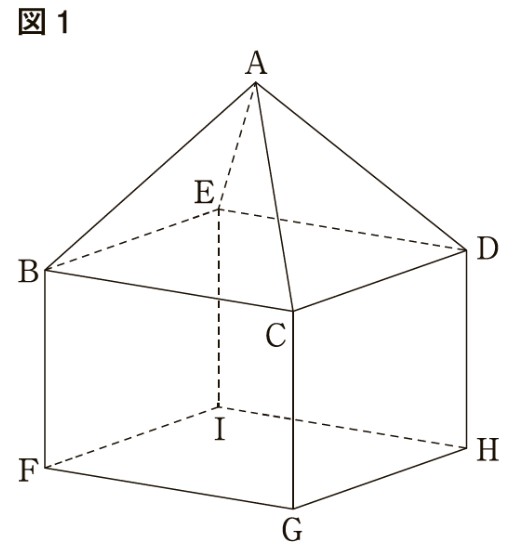
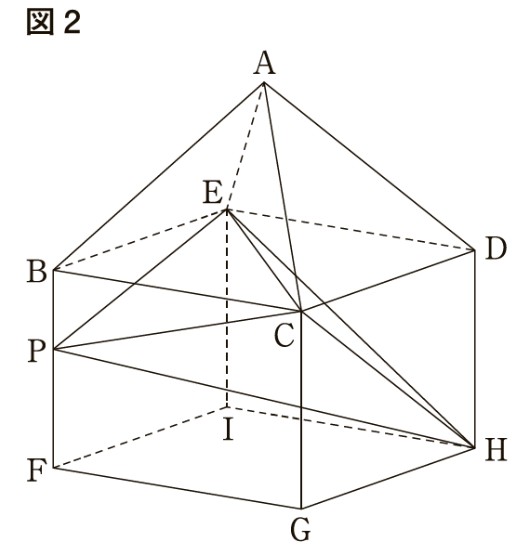
図2は,図1における点,を,線分,を延長した直線上に となるようにそれぞれとったものである。
図2においても,四角形は平行四辺形である。このことは,上の証明の下線部ア~カのうち,いずれか1つをかき直すことで証明することができる。
上の証明を,図2における「四角形は平行四辺形である」ことの証明とするには,どの下線部をかき直せばよいか。ア~カから1つ選び,記号をかき,その下線部を正しくかき直せ。
8
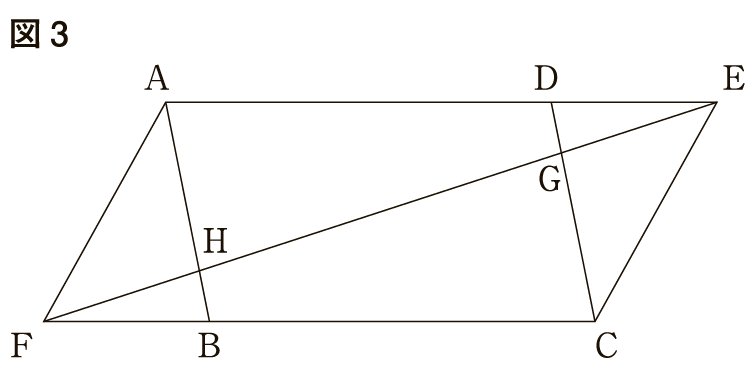
(2) 図3は,図2において,対角線と線分,線分との交点をそれぞれ,としたものである。
図3において, であることを証明せよ。
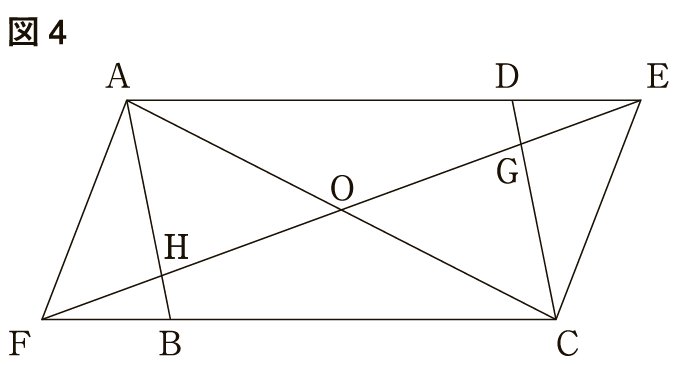
(3) 図4は,図3において, となる場合を表しており,対角線と対角線との交点をとしたものである。
平行四辺形の面積がのとき,四角形の面積を求めよ。






![]() )を
)を![]() )に
)に